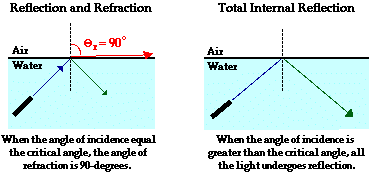
le, ---> --->
le, ---> ---> ce is greater than the critical angle, total internal reflection will occur.
ce is greater than the critical angle, total internal reflection will occur.Then we were assigned to read pages 344-349 "Applications of the Critical Angle and the Total Internal Reflection", then you had to choose two of the applications you read and had to summarize each of them. The applications were :

Mirrors and Prisms- When light reflects off a mirror, about 10% of the light is lost. For good periscopes or binoculars have glass prisms that use total internal reflection. Almost no light is lost.
 Mirages- there are two types of mirages inferior and superior. Inferior is when you are driving on a hot day and it seem's that there is water up ahead on the road, when really all it is, is an illusion. It is caused by when cool layers of air lie above warm layer of air. what your eyes see is a virtual image of the sky below the road.
Mirages- there are two types of mirages inferior and superior. Inferior is when you are driving on a hot day and it seem's that there is water up ahead on the road, when really all it is, is an illusion. It is caused by when cool layers of air lie above warm layer of air. what your eyes see is a virtual image of the sky below the road.  There is also superior mirages which makes the object seem more up and farther away when really it is just denser layer's of air lie below less dense layer's. In this case light refracts towards the denser air, causing the image to look displaced upward.
There is also superior mirages which makes the object seem more up and farther away when really it is just denser layer's of air lie below less dense layer's. In this case light refracts towards the denser air, causing the image to look displaced upward.